[
bit-dp backtracking dfs Leetcode 1659. Maximize Grid Happiness
https://leetcode.com/problems/maximize-grid-happiness
Let us us dynamic programming with the following states:
index: number of cell in our grid, going from0tomn-1: from top left corner, line by line.rowis the next row filled with elements0,1(for introvert) or2(for extravert): see on my diagramm.Iis number of interverts we have left.Eis number of extraverts we have left.
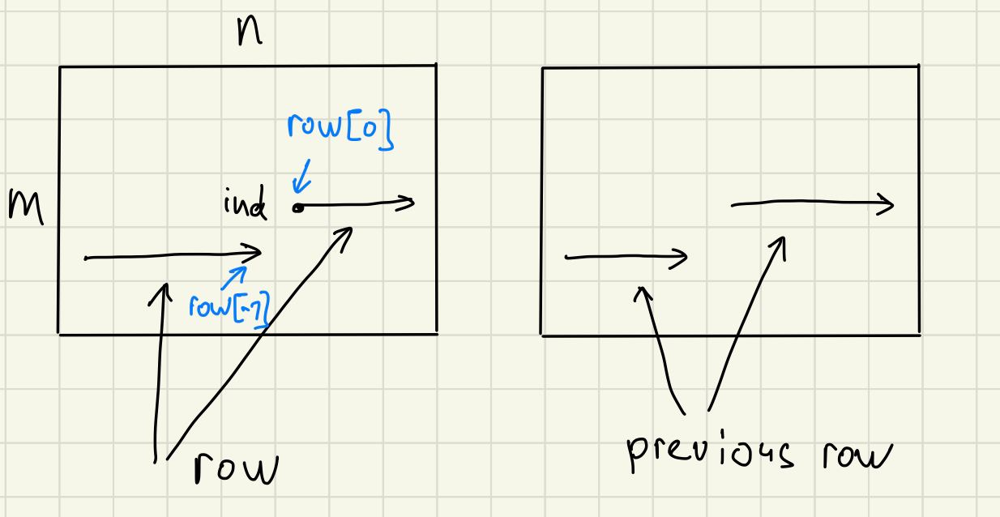
Now, let us fill out table element by element, using dp function:
- First of all, if we reached
index == -1, we return 0, it is our border case. - Compute
RandCcoordinates of our cell. - Define
neibs: it is parameters for our recursion: fist element is what we put into this element:0,1or2, second and third elements are new coordinates and last one is gain. - Now, we have
3possible cases we need to cover: new cell is filled with0,1or2and for each of these cases we need to calculateans: a) this isdpfor our previous row, shifted by one b) gain we need to add when we add new intravert / extravert / empty c) check right neighbor (if we have any) and addfine: for example if we have 2 introverts, both of them are not happy, so we need to add-30-30, if we have one introvert and one extravert, it is20-30and if it is two extraverts it is20+20. d) do the same for down neigbor if we have any (see illustration for help)
Finally, we just return dp(m*n-1, tuple([0]*n), I, E)
Complexity: time complexity is O(m*n*I*E*3^n), because: index goes from 0 to mn-1, row has n elements, each of them equal to 0, 1 or 2.
class Solution:
def getMaxGridHappiness(self, m, n, I, E):
InG, ExG, InL, ExL = 120, 40, -30, 20
fine = [[0, 0, 0], [0, 2*InL, InL+ExL], [0, InL+ExL, 2*ExL]]
@lru_cache(None)
def dp(index, row, I, E):
if index == -1: return 0
R, C, ans = index//n, index%n, []
neibs = [(1, I-1, E, InG), (2, I, E-1, ExG), (0, I, E, 0)]
for val, dx, dy, gain in neibs:
tmp = 0
if dx >= 0 and dy >= 0:
tmp = dp(index-1, (val,) + row[:-1], dx, dy) + gain
if C < n-1: tmp += fine[val][row[0]] #right neighbor
if R < m-1: tmp += fine[val][row[-1]] #down neighbor
ans.append(tmp)
return max(ans)
if m < n: m, n = n, m
return dp(m*n-1, tuple([0]*n), I, E)
If you like the solution, you can upvote it on leetcode discussion section: Problem 1659