https://leetcode.com/problems/distribute-candies-to-people

There are different ways how you can handle this problem, I prefer mathematical way. Let us define k = num_people and n = candies and try to understand how many candies we need to give to i-the person.

1 2 3 … k
k+1 k+2 k+3 … 2k
… … … … …
sk+1 … sk+i    

We need to find the biggest s, such that the sum of numbers before is less or equal to n. Let us compute it:

1. First row: k(k+1)/2, sum of arithmetic progression.

2. Second row: k(k+1)/2 + k^2.

3. Third row: k(k+1)/2 + 2*k^2. …

s-1. k(k+1)/2 + (s-1)*k^2.

s. s*k*i + i(i+1)/2.

Let us evaluate this sum and solve quadratic inequality:

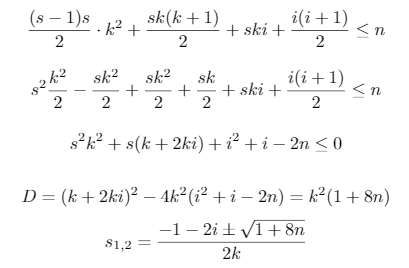
image

So, we have root s = ((-1-2*i) + sqrt(1+8*n))/(2*k) and we need to find the biggest integer number which is less than s, let us define it t = floor(s). Now, how many candies we need to give to this person? It is i + (k+i) + ... + (sk+i) = i*(t+1) + k*t*(t+1)//2. Finally, we need to find the last person, who gets the rest of the candies. How we can do it? I evaluate difference s - floor(s) and choose the person with the biggest difference.

Complexity: time and space complexity is O(k), where k is number of people.

class Solution:
    def distributeCandies(self, candies, num_people):
        k, n = num_people, candies
        alloc = [0]*k
        Final = (0, 0)
        for i in range(1, k+1):
            s = ((-1-2*i) + sqrt(1+8*n))/(2*k)
            t = floor(s)
            alloc[i-1] = i*(t+1) + k*t*(t+1)//2
            Final = max(Final, (s-floor(s), i)) 
            
        alloc[Final[1]-1] += (n - sum(alloc))
            
        return alloc

If you like the solution, you can upvote it on leetcode discussion section: Problem 1103