https://leetcode.com/problems/image-overlap

If you have some data science backgroud, as I have, then it is not difficult to think about convolutions, when you see this problem. Let me remind you, what 2d convolution is: this is special operations between matrices, which use the notion of sliding window. For each window we need to evaluate sum of products of all elements in this window and the second matrix, which is called filter. For example for thise red matrix we have 1*1 + 0*0 + 0*1 + 1*0 + 1*1 + 0*0 + 1*1 + 1*0 + 1*1 = 4.

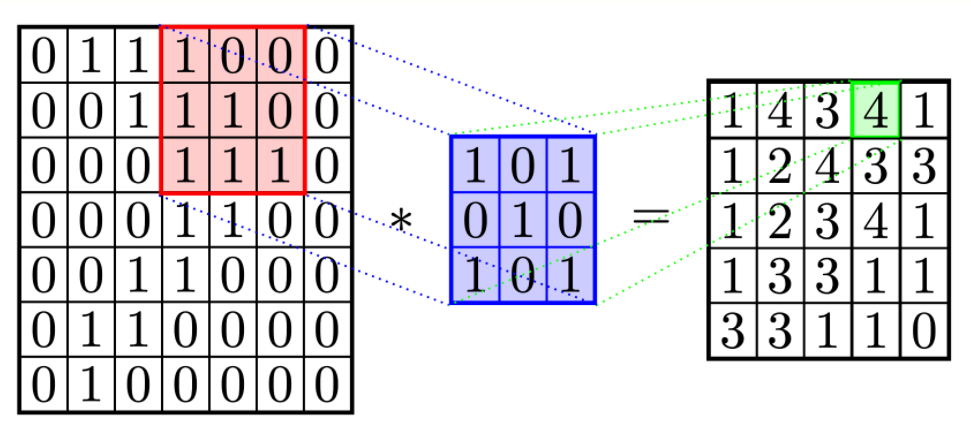
image

Now, notice, that each value in the resulting matrix will show how many overlaps we have for shifted image! However there is couple of points we need to deal with:

  1. Let as add a lot of zeros to the B matrix: by this I mean, if it had n x n size, let us make it 3n x 3n with original matrix B in the middle and zeroes outside. Why we need this? Because we need to consider all possible shifts, including n shift to the right, left, up and down.
  2. Also, I want to use scipy.ndimage library, which have convolve function, exactly what we need. But before we use it, we need to rotate image A by 180 degrees! This step was not obvious for me, but this is because convolution is defined a bit different in different sources.
  3. Finally, we return maximum of resulting matrix.

Complexity: Let n be size of images. Then to evaluate one element of resulting image we need to make n^2 multiplications and summations. We have O(n^2) elements in the end, so we have O(n^4) complexity. Memory is O(n^2).

from scipy.ndimage import convolve
import numpy as np

class Solution:
    def largestOverlap(self, A, B):
        B = np.pad(B, len(A), mode='constant', constant_values=(0, 0))
        return np.amax(convolve(B, np.flip(np.flip(A,1),0), mode='constant'))

If you like the solution, you can upvote it on leetcode discussion section: Problem 0835