https://leetcode.com/problems/maximum-width-of-binary-tree

In this problem we need to find maximum width of binary tree, so we need to use some tree traversal algorithm. BFS or DFS? I prefer to use BFS, because it emulate level by level traversal. While we traverse we need to keep some information about our node: its level, but also its num, which is number in level if this level was full. So, let us keep 3 informations for each node: [num, level, node]. How we change this information, when we traverse tree? We increase level by 1, and for num, for left children we evaluate 2*num and for the right we evaluate 2*num + 1. You can see how it works on the following tree (here in brackets I show 2 numbers : [num, level]. For example for node with [num, level] = [5, 3], left children will have [10, 4] and right [11, 4].

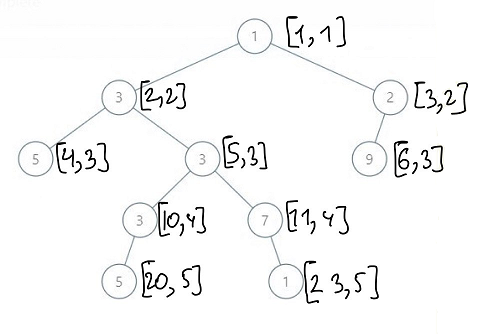
image

So, we traverse our tree, using BFS, keep this information. Also we have level_old and num_old variable, which keep information for the first (the most left) node on each level, using this values we can understand if new level is started, and if started, we update it and for each new node we can evaluate current width of traversing layer.

Complexity: time complexity is O(n), where n is number of nodes, because we traverse our tree, using bfs. Space complexity is O(w), where w is the biggest number of nodes in level, because we need to keep our queue. Potentially it is equal to O(n). If we use DFS, then space complexity will be O(h), where h is height of tree.

class Solution:
    def widthOfBinaryTree(self, root):
        level_old, num_old, max_width = 1, 1, 0
        queue = deque([[level_old,num_old,root]])

        while queue:    
            [num, level, node] = queue.popleft()
            if level > level_old:
                level_old, num_old = level, num
                
            max_width = max(max_width, num - num_old + 1)
            if node.left:  queue.append([num*2,  level+1, node.left])
            if node.right: queue.append([num*2+1,level+1, node.right])
                
        return max_width

If you like the solution, you can upvote it on leetcode discussion section: Problem 0662