https://leetcode.com/problems/random-pick-with-weight

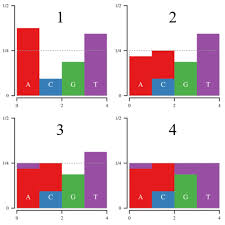
Probably you already aware of other solutions, which use linear search with O(n) complexity and binary search with O(log n) complexity. When I first time solved this problem, I thought, that O(log n) is the best complexity you can achieve, howerer it is not! You can achieve O(1) complexity of function pickIndex(), using smart mathematical trick: let me explain it on the example: w = [w1, w2, w3, w4] = [0.1, 0.2, 0.3, 0.4]. Let us create 4 boxes with size 1/n = 0.25 and distribute original weights into our boxes in such case, that there is no more than 2 parts in each box. For example we can distribute it like this:

  1. Box 1: 0.1 of w1 and 0.15 of w3
  2. Box 2: 0.2 of w2 and 0.05 of w3
  3. Box 3: 0.1 of w3 and 0.15 of w4
  4. Box 4: 0.25 of w4

(if weights sum of weights is not equal to one, we normalize them first, dividing by sum of all weights).

image this method has a name: https://en.wikipedia.org/wiki/Alias_method , here you can see it in more details.

Sketch of proof There is always a way to distribute weights like this, it can be proved by induction, there is always be one box with weight <=1/n and one with >=1/n, we take first box in full and add the rest weight from the second, so they fill the full box. Like we did for Box 1 in our example: we take 0.1 - full w1 and 0.15 from w3. After we did it we have w2: 0.2, w3: 0.15 and w4: 0.4, and again we have one box with >=1/4 and one box with <=1/4.

Now, when we created all boxes, to generate our data we need to do 2 steps: first, to generate box number in O(1), because sizes of boxes are equal, and second, generate point uniformly inside this box to choose index. This is working, because of Law of total probability.

Complexity. Time and space complexity of preprocessing is O(n), but we do it only once. Time and space for function pickIndex is just O(1): all we need to do is generate uniformly distributed random variable twice!

Code is not the easiest one to follow, but so is the solution. First, I keep two dictionaries Dic_More and Dic_Less, where I distribute weights if they are more or less than 1/n. Then I Iterate over these dictionaries and choose one weight which is more than 1/n, another which is less, and update our weights. Finally when Dic_Less is empty, it means that we have only elements equal to 1/n and we put them all into separate boxes. I keep boxes in the following way: self.Boxes is a list of tuples, with 3 numbers: index of first weight, index of second weight and split, for example for Box 1: 0.1 of w1 and 0.15 of w3, we keep (1, 3, 0.4). If we have only one weight in box, we keep its index.

class Solution:
  def __init__(self, w):
    ep = 10e-5
    self.N, summ = len(w), sum(w)
    weights = [elem/summ for elem in w]
    Dic_More, Dic_Less, self.Boxes = {}, {}, []
    
    for i in range(self.N):
      if weights[i] >= 1/self.N:
        Dic_More[i] = weights[i]
      else:
        Dic_Less[i] = weights[i]

    while Dic_More and Dic_Less:
      t_1 = next(iter(Dic_More))
      t_2 = next(iter(Dic_Less))
      self.Boxes.append([t_2,t_1,Dic_Less[t_2]*self.N])

      Dic_More[t_1] -= (1/self.N - Dic_Less[t_2])
      if Dic_More[t_1] < 1/self.N - ep:
        Dic_Less[t_1] = Dic_More[t_1]
        Dic_More.pop(t_1)
      Dic_Less.pop(t_2)
    
    for key in Dic_More: self.Boxes.append([key])

  def pickIndex(self):
    r = random.uniform(0, 1)
    Box_num = int(r*self.N)
    if len(self.Boxes[Box_num]) == 1:
      return self.Boxes[Box_num][0]
    else:
      q = random.uniform(0, 1)
      if q < self.Boxes[Box_num][2]:
        return self.Boxes[Box_num][0]
      else:
        return self.Boxes[Box_num][1]

If you like the solution, you can upvote it on leetcode discussion section: Problem 0528