https://leetcode.com/problems/generate-random-point-in-a-circle

Imagine first special case for this problem: we have circle with radius equal to 1 and coordinates of center is (0, 0). Let us use polar coordinates: x = R * cos(theta) y = R * sin(theta).

closed_paren

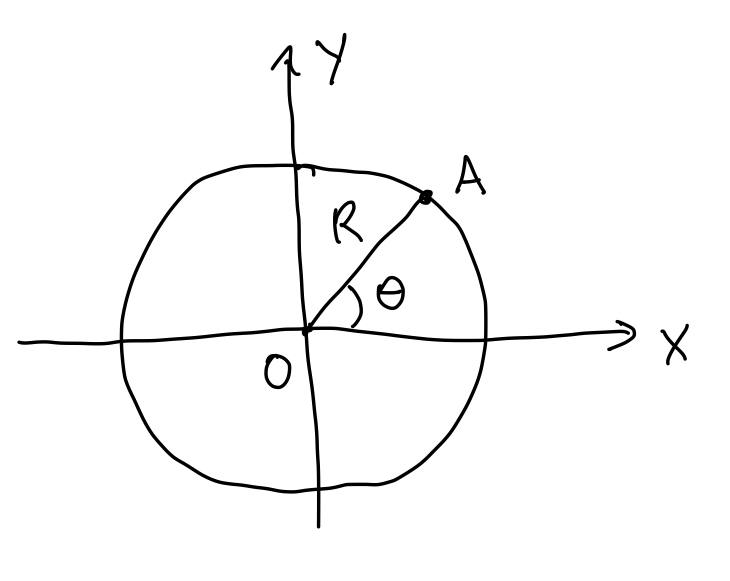
Here R is distance between our point (call it A) and the origin (call it O). theta is angle between OA and axis OX. Why it is good idea to go to polar coordinates here? Because in polar coordiantes unity circle can be written as: R <= 1 0 <= theta <= 2*pi.

Now we need to answer two qustions: how to generate R and how to generate theta.

  1. About theta it is quite obvious: we do it uniformly.
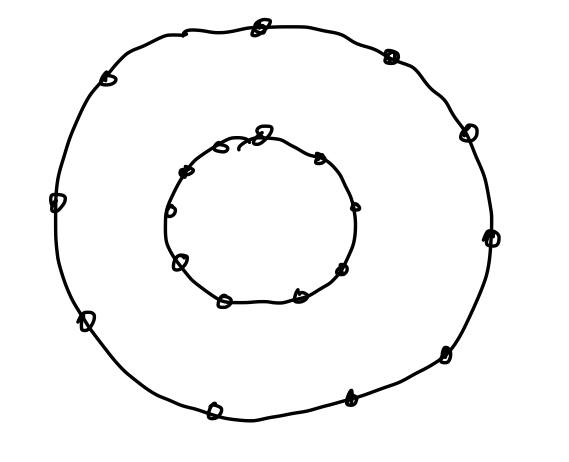
  2. About R it is not obvious: if we do it uniformly, there will be more points closer if we generate it in uniform way. Look at this intuition: let us fix R = 1 and generate 10 points, then fix R = 0.5 and generate 10 more points. What you can see? Distance between points on the big circle is in average 2 times bigger, than between 2 points on smaller circle. It actually means, that for small circle you need to generate only 5 points, not 10, and by this logic if you have x points for circle with R = 1, you need x*R points for smaller radius.

closed_paren

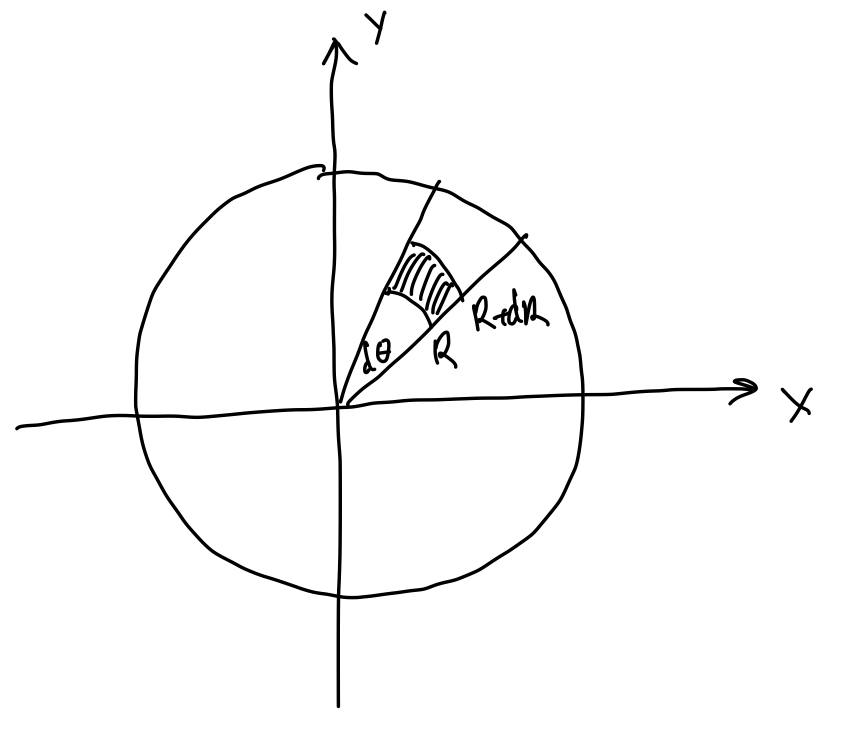
This was intuition, now let go into mathematics: what does uniform distribution means, that if we choose small element inside our circle, than probability to get inside this element should be proportional to area of this element. Let us define F(R) cumulative distribution function (cdf) for radius. Then by definition probability to get between R and R + dR is equal to F(R + dR) - F(R) = f(R)*dR, where f(R) is probability density function (pdf), so probability to get into this small region is f(R)* dR * dTheta. From other point of view, area of this region can be calclated as [(R+dR)^2 - R^2]*dTheta = 2*R*dR*dTheta. From here we get, that f(R) = c*R for some constant c (because we say it is proportional, not equal). Now, F'(R) = f(R), so F(R) = c*R^2 (here c is another conatant). Now the question is how you generate data such that cumulative function is proportional to R^2. The answer is Inverse transform sampling (check wikipedia), where idea is given uniform distribution generate data from any distribution F(R): we need to generate R from uniform distrubution and than apply inverse function, that is we have sqrt(uniform(0,1)) in the end.

closed_paren

Complexity: time and space complexity is just O(1).

class Solution:
    def __init__(self, radius, x_center, y_center):
        self.r, self.x, self.y = radius, x_center, y_center

    def randPoint(self):
        theta = uniform(0,2*pi)
        R = self.r*sqrt(uniform(0,1))
        return [self.x + R*cos(theta), self.y + R*sin(theta)]

If you like the solution, you can upvote it on leetcode discussion section: Problem 0478