tree recursion hash table Leetcode 0437. Path Sum III
https://leetcode.com/problems/path-sum-iii
If we can have any solution, that this problem is indeed medium. However if we wan to have O(n) time solution, in my opinion it is more like hard, because we need to use dfs + hash table in the same time.
First of all, let us evaluate cumulative sum of our tree, what does it mean? Here an example: for each node we evaluate sum of path from this node to root.
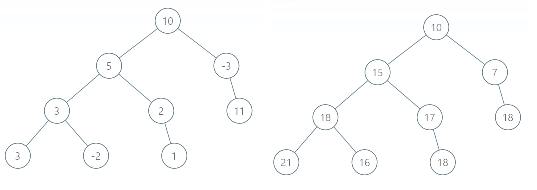
Also we evaluate number of nodes in our tree. What we need to find now? Number of pairs of two nodes, one of them is descendant of another and difference of cumulative sums is equal to sum. Let me explain my dfs(self, root, sum) function:
- If we reached
None, just go back. - We have
self.counthash table, where we putroot.val + sum: number we are looking for when we visited this node: for example if we are in node with value15now (see our example), then we want to find node with values15+8inside. - Also, we add to our final result number of solution for our
root.val. - Run recursively our
dfsfor left and right children - Remove our
root.val + sumfrom our hash table, because we are not anymore inrootnode.
Now, let us consider our pathSum(self, root, sum) function:
- If tree is empty, we return
0 - Define some global variables.
- Run our
cumSumfunction to evaluate cumulative sums - Run
dfsmethod. - In the end we need to subtract
self.n*(sum == 0)from our result. Why? Because ifsum = 0, then we will count exactlyself.nempty cumulative sums, which consist of zero elements.
Complexity: Time complexity to evaluate cumulative sums is O(n). The same time complexity is for dfs function. Space complexity is also O(n), because we need to keep this amount of information in our count hash table.
class Solution:
def cumSum(self, root):
self.n += 1
for child in filter(None, [root.left, root.right]):
child.val += root.val
self.cumSum(child)
def dfs(self, root, sum):
if not root: return None
self.count[root.val + sum] += 1
self.result += self.count[root.val]
self.dfs(root.left, sum)
self.dfs(root.right, sum)
self.count[root.val + sum] -= 1
def pathSum(self, root, sum):
if not root: return 0
self.n, self.result, self.count = 0, 0, defaultdict(int)
self.cumSum(root)
self.count[sum] = 1
self.dfs(root, sum)
return self.result - self.n*(sum == 0)
Update: thanks @rkmd for pointing out that we do not really need to evaluate cumlative sums, we can do in on the fly. Also if we do it on the fly, we do not need to check case if sum == 0. Here is the code:
class Solution:
def dfs(self, root, sum, root_sum):
if not root: return None
root_sum += root.val
self.result += self.count[root_sum]
self.count[root_sum + sum] += 1
self.dfs(root.left, sum, root_sum)
self.dfs(root.right, sum, root_sum)
self.count[root_sum + sum] -= 1
def pathSum(self, root, sum):
self.result, self.count = 0, defaultdict(int)
self.count[sum] = 1
self.dfs(root, sum, 0)
return self.result
If you like the solution, you can upvote it on leetcode discussion section: Problem 0437