https://leetcode.com/problems/count-complete-tree-nodes Here we are given, that our tree is **complete** and we need to use this property to make it faster. Let us consider the following tree:

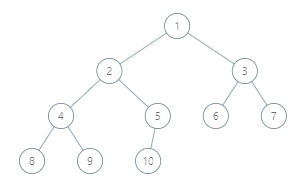
image

  1. I denoted values for nodes in the way of how we are going to count them, note that it does not matter in fact what is inside.
  2. First step is to find the number of levels in our tree, you can see, that levels with depth 0,1,2 are full levels and level with depth = 3 is not full here.
  3. So, when we found that depth = 3, we know, that there can be between 8 and 15 nodes when we fill the last layer.
  4. How we can find the number of elements in last layer? We use binary search, because we know, that elements go from left to right in complete binary tree. To reach the last layer we use binary decoding, for example for number 10, we write it as 1010 in binary, remove first element (it always will be 1 and we not interested in it), and now we need to take 3 steps: 010, which means left, right, left.

Complexity. To find number of layers we need O(log n). We also need O(log n) iterations for binary search, on each of them we reach the bottom layer in O(log n). So, overall time complexity is O(log n * log n). Space complexity is O(log n).

Code I use auxiliary funcion Path, which returns True if it found node with given number and False in opposite case. In main function we first evaluate depth, and then start binary search with interval 2^depth, 2^{depth+1} - 1. We also need to process one border case, where last layer is full.

class Solution:
    def Path(self, root, num):
        for s in bin(num)[3:]:
            if s == "0": 
                root = root.left
            else:
                root = root.right
            if not root: return False
        return True
        
    def countNodes(self, root):
        if not root: return 0
        
        left, depth = root, 0
        while left.left:
            left, depth = left.left, depth + 1

        begin, end = (1<<depth), (1<<(depth+1)) - 1
        if self.Path(root,end): return end
        
        while begin + 1 < end:
            mid = (begin + end)//2
            if self.Path(root, mid):
                begin = mid
            else:
                end = mid
        return begin

If you like the solution, you can upvote it on leetcode discussion section: Problem 0222