Problem statement

https://leetcode.com/problems/path-sum-ii/

Solution

This is classical dfs problem: let use dfs(node, sm) function, which have parameters:

  1. node is current node we are in now.
  2. sm is value we need to get.
  3. output are all possible paths we can get, here I keep them inverted, because it is faster to add to the end of list.

When we traverse our tree, we need to do the following:

  1. Check if we go outside tree, in this case we return [].
  2. Check if we reached leaf, and value in this leaf is equal to node.val, in this case return [[node.val]].
  3. Run function recursively for left and right children. Not that some of them can be empty, in thic case answer for this child will be [].
  4. Finally, return list of lists for both left and right children.

Complexity

Complexity of pure dfs part is just O(n), what is more interesting is complexity of this dfs where we need to keep lists. If we consider balanced tree, than we can have O(n) solutions, which of which have O(log n) length, so time and space complexity will be O(n log n). However it can go upto O(n^2), see the following example:

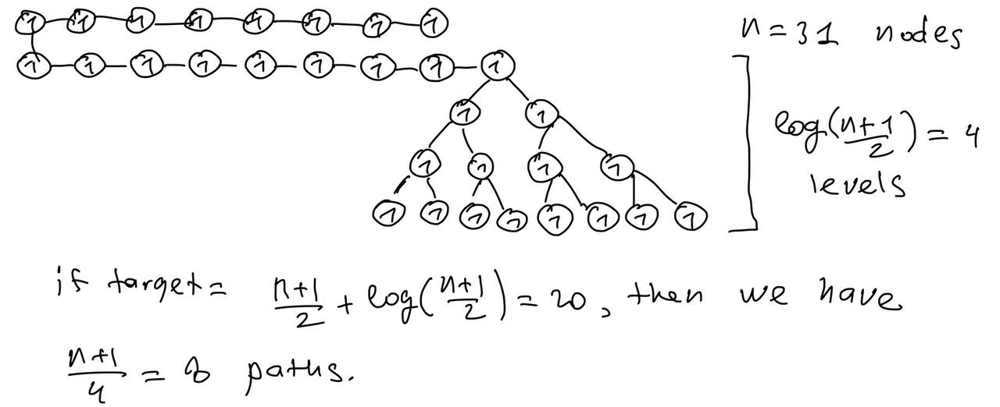
Let us have tree with n nodes, such that first it is single line with length n/2: a1 -> a2 -> ... a_(n//2) -> (full tree on n/2 nodes). All values in all nodes equal to 1. Then there will be n//4 leafs and path to each leaf has n//2+log(n//2) = O(n) length, so all paths will take n//4*(n//2 + log(n//2)) = O(n^2) time and space complexity. See image for more details.

image

Code

class Solution:
    def pathSum(self, root, sm):
        def dfs(node, sm):
            if not node: return []
            if not node.left and not node.right and sm == node.val:
                return [[node.val]]
           
            lft = dfs(node.left, sm - node.val)
            rgh = dfs(node.right, sm - node.val)
            return [cand + [node.val] for cand in lft + rgh]
            
        return [s[::-1] for s in dfs(root, sm)]