Leetcode 0106. Construct Binary Tree from Inorder and Postorder Traversal

https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal

To solve this problem we need to understand, what is inorder and what is postorder traversal of tree. Let me remind you:

1. inorder traversal is when you visit left, root, right, where left is left subtree, root is root node and right is right subtree.
2. postorder traversal is when you visit left, right, root.

We can see that in postorder traverasl root will be in the end, so we take this element and we need to find it in inorder array. Then we need to call function recursively on the left subtree and right subtree. It is easier said that done, so let us introduce function helper(post_beg, post_end, in_beg, in_end), which has 4 parameters:

1. post_beg and post_end are indices in original postorder array of current window. Note, that we use python notation, so post_end points to one element after the end.
2. in_beg and in_end are indices in original inorder array of current window. We again use python notation, where in_end points to one element after the end.

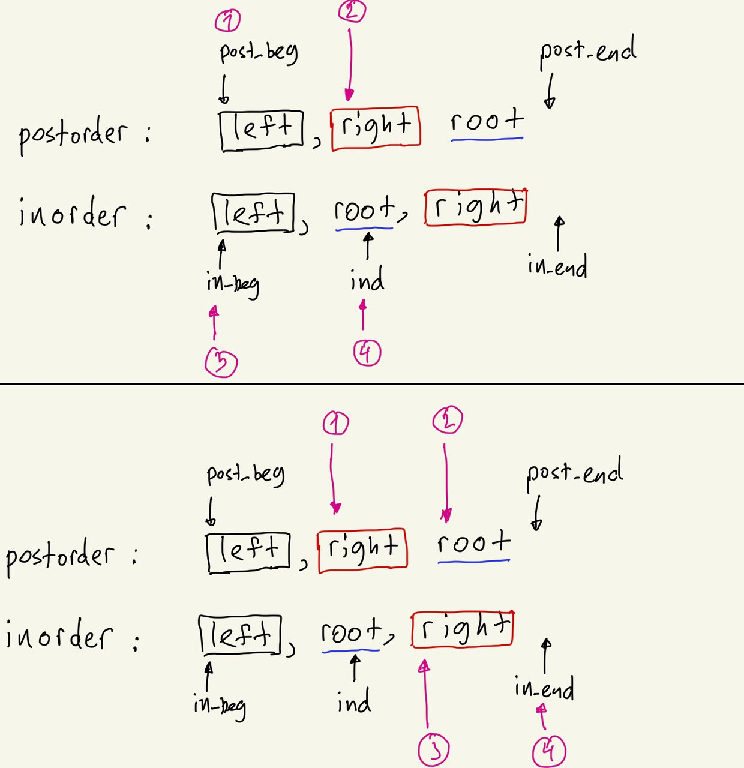
Then what we need to do is to find indices of left part and right part. First of all, evaluate ind = dic[postorder[post_end-1]], where we create dic = {elem: it for it, elem in enumerate(inorder)} for fast access to elements. Now, look at the next two images:

On the first one 1, 2, 3, 4 in circles are equal to post_beg, post_beg + ind - in_beg, in_beg, ind. Why? 1 should point to beginning of left in postorder, so it is equal to post_beg. 2 should point to one element after the end of left, so we need to know the length of left, we can find it from inorder array, it is ind - in_beg. So, finally, point 2 is equal to post_beg + ind - in_beg. Point 3 should point to start of left in inorder array, that is in_beg and point 4 should point to element after the end of left in inorder array, that is ind.

On the second one 1, 2, 3, 4 in circles are equal to post_end - in_end + ind, post_end - 1, ind + 1, in_end. The logic is similar as for left parts, but here we look into right arrays.

Complexity: Time complexity is O(n), because we traverse each element only once and we have O(1) complexity to find element in dic. Space complexity is also O(n), because we keep additional dic with this size.

class Solution:
    def buildTree(self, inorder, postorder):
        def helper(post_beg, post_end, in_beg, in_end):
            if post_end - post_beg <= 0: return None
            ind = dic[postorder[post_end-1]]

            root = TreeNode(inorder[ind])  
            root.left  = helper(post_beg, post_beg + ind - in_beg, in_beg, ind)
            root.right = helper(post_end - in_end + ind, post_end - 1, ind + 1, in_end)
            return root
        
        dic = {elem: it for it, elem in enumerate(inorder)}  
        return helper(0, len(postorder), 0, len(inorder))

If you like the solution, you can upvote it on leetcode discussion section: Problem 0106