https://leetcode.com/problems/search-in-rotated-sorted-array-ii

The idea here is to use both binary search and dfs: each time we compare nums[mid] and nums[end] and we can have several options:

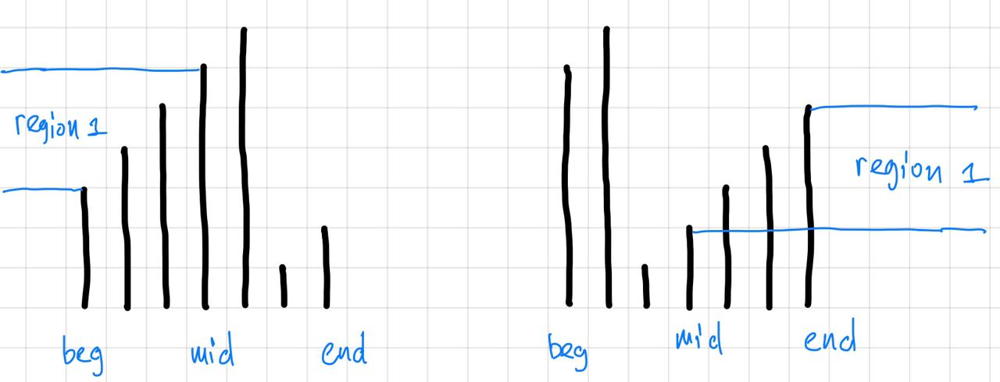
  1. nums[mid] > nums[end], for example data can look like 3,4,5,6,7,1,2. Then we need to check conditions: a. If nums[end] < target <= nums[mid], then it means, that we need to look in the left half of our data: see region 1 on the left image. b. Else means, that we need to look in the right half of data.
  2. nums[mid] < nums[end], for example data can look like 6,7,1,2,3,4,5. Then we need to check conditions: a. if nums[mid] < target <= nums[end], then it means, that we need to look in the right half of our data: see region 1 on the right image. b. Else means, that we need to look in the left half of data.
  3. In this problem it can happen, that nums[mid] == nums[end], and in this case we do not know where to find our number, so we just look for it in both halves.

Complexity: if we do not have any duplicates, it is for sure O(log n). If we have any, it can be potentially O(n) for cases like 111111111111121111: where we do not know the place of 2 and we basically need to traverse all elements to find it.

image

class Solution:
    def search(self, nums, target):
        def dfs(beg, end):
            if end - beg <= 1: return target in nums[beg: end+1]
            
            mid = (beg + end)//2
            if nums[mid] > nums[end]:   # eg. 3,4,5,6,7,1,2
                if nums[end] < target <= nums[mid]:
                    return dfs(beg, mid)
                else:
                    return dfs(mid + 1, end)
            elif nums[mid] < nums[end]: # eg. 6,7,1,2,3,4,5
                if nums[mid] < target <= nums[end]:
                    return dfs(mid + 1, end)
                else:
                    return dfs(beg, mid)
            else:
                return dfs(mid+1, end) or dfs(beg, mid)
    
        return dfs(0, len(nums)-1)

If you have any questions, feel free to ask. If you like solution and explanations, please Upvote!

If you like the solution, you can upvote it on leetcode discussion section: Problem 0081