dp bit-dp Leetcode 1931. Painting a Grid With Three Different Colors
Problem statement
https://leetcode.com/problems/painting-a-grid-with-three-different-colors/
Solution 1
The idea is to go row by row and check that we do not have conflicts of colors in each row and between rows.
Cis all candidates for row, that is all rows, such that we do not have conflicts among horizontal adjacent cells.- Also create dictionarly
d: where for each candidate we collect all possible options for the next line such that we do not have vertical conflicts. - Finally, we go level by level and for each
c1among candidates and then for eachc2 in d[c1], we update number of options fordp2[c2]. In the end of iteration we updatedp = dp2.
Complexity
We have O(3^m * m) complexity to generate C. In fact we will have 3*2^(m-1) options for each row. Then when we check all pairs we do O(9^2^(2m-2) * m) = O(4^m * m) ways. Then we have O(4^m * m) complexity for each level, so total time complexity is O(4^m * n * m). Space complexity is O(4^m).
Code
class Solution:
def colorTheGrid(self, m, n):
C = [c for c in product([0,1,2], repeat = m) if all(x!=y for x,y in zip(c, c[1:]))]
MOD, dp, d = 10**9 + 7, Counter(C), defaultdict(list)
for c1, c2 in product(C, C):
if all(x != y for x, y in zip(c1, c2)):
d[c1].append(c2)
for _ in range(n-1):
dp2 = Counter()
for c1 in C:
for c2 in d[c1]:
dp2[c2] = (dp2[c2] + dp[c1]) % MOD
dp = dp2
return sum(dp.values()) % MOD
Solution 2
Actually, there is solution with better complexity! The idea is Problem 1659. Maximize Grid Happiness , you can find more explanations here: https://leetcode.com/problems/maximize-grid-happiness/discuss/936467/Python-Short-and-clean-dp-with-diagram-expained
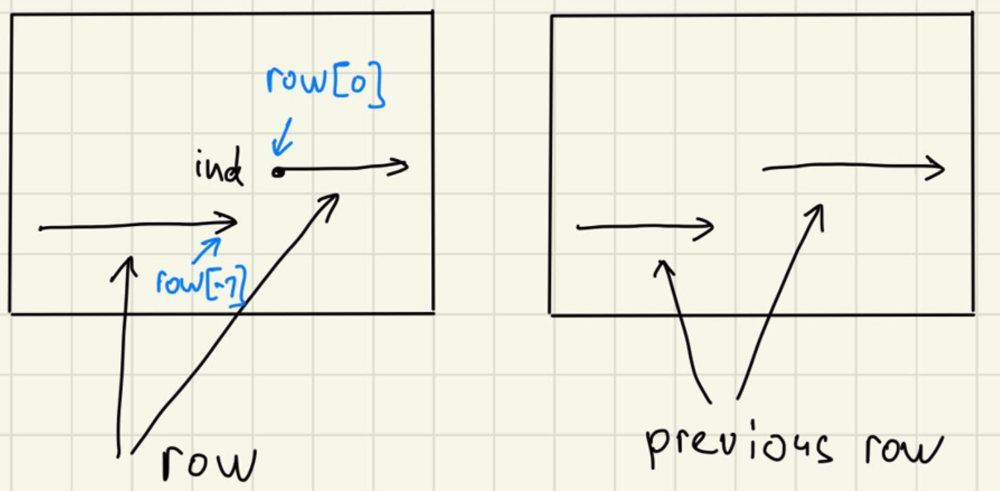
We use so-called dp with broken profile, and on each step we try to add one more element, checking two neigbours.
Complexity:
We have mn states for index and O(2^m) states for row. So, we have in total O(2^m * m * n) states, which of them have length O(m). So, total space and time complexity here is O(2^m * m^2*n)
Code 1
class Solution:
def colorTheGrid(self, m, n):
@lru_cache(None)
def dp(index, row):
if index == -1: return 1
R, C = divmod(index, m)
ans, allowed = 0, {0, 1, 2}
if C < m - 1: allowed.discard(row[0])
if R < n - 1: allowed.discard(row[-1])
for val in allowed:
ans += dp(index-1, (val,) + row[:-1])
return ans % MOD
MOD = 10**9 + 7
return dp(m*n-1, tuple([3]*m)) % MOD
Complexity can be reduced to just O(2^m * n * m) if we use bitmasks instead of tuples: 00, 01, 10, 11 represents 0, 1, 2, 3, and we spend two bits for each of m element of row, so we keep number with 2m bits. Because of lru_cache we use here we have quite big armotization constant, so to make it really fast you can use classical table dp.
Update Actually, number of states is approximately O(2^m * n * m * 2.25), because our row consist of two parts, each of which can start from any color and then we can take always no more than 2 options.
Code 2
class Solution:
def colorTheGrid(self, m, n):
@lru_cache(None)
def dp(index, row):
if index == -1: return 1
R, C = divmod(index, m)
ans, allowed = 0, {0, 1, 2}
if C < m - 1: allowed.discard(row >> (2*m-2))
if R < n - 1: allowed.discard(row & 3)
for val in allowed:
ans += dp(index-1, (row >> 2) + (val<<(2*m-2)))
return ans % MOD
MOD = 10**9 + 7
return dp(m*n-1, (1<<(2*m)) - 1) % MOD
Actually we can implement the same logic without recursion, and I thought that it will make code several times faster, but no it is not. I need to inverstigate why, does anybody have any ideas? One theory is that m is quite small here, and because of hidden constants are quite big, we can not bead the first method.
Code 3
class Solution:
def colorTheGrid(self, m, n):
dp, MOD = {(1<<(2*m)) - 1: 1}, 10**9 + 7
for index in range(m*n-1, -1, -1):
dp2 = Counter()
R, C = divmod(index, m)
for row in dp:
allowed = {0, 1, 2}
if C < m - 1: allowed.discard(row >> (2*m-2))
if R < n - 1: allowed.discard(row & 3)
for val in allowed:
row2 = (row >> 2) + (val<<(2*m-2))
dp2[row2] = (dp2[row2] + dp[row]) % MOD
dp = dp2
return sum(dp.values()) % MOD
Update as it happen, indeed when we increase m with fixed n = 1000 and we an fell difference starging from m = 10.
| m | Solution 1 time | Solution 2 time |
|---|---|---|
| 1 | 0.007 | 0.016 |
| 2 | 0.015 | 0.041 |
| 3 | 0.032 | 0.130 |
| 4 | 0.094 | 0.327 |
| 5 | 0.290 | 0.847 |
| 6 | 0.859 | 2.006 |
| 7 | 2.612 | 4.638 |
| 8 | 7.965 | 10.73 |
| 9 | 24.51 | 24.21 |
| 10 | 75.61 | 56.07 |
| 11 | 235.0 | 125.2 |
| 12 | 730.2 | 279.6 |
If you have any questions, feel free to ask. If you like solution and explanations, please Upvote!