design hash table Leetcode 0705. Design HashSet
https://leetcode.com/problems/design-hashset
The goal of this problem is to create simple hash function, not using build-in methods. One of the simplest, but classical hashes are so-called Multiplicative hashing: https://en.wikipedia.org/wiki/Hash_function#Multiplicative_hashing.
The idea is to have hash function in the following form.
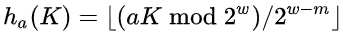
Here we use the following notations:
Kis our number (key), we want to hash.ais some big odd number (sometimes good idea to use prime number) I choosea = 1031237without any special reason, it is just random odd number.mis length in bits of output we wan to have. We are given, that we have no more than10000operations overall, so we can choose suchm, so that2^m > 10000. I chosem = 15, so in this case we have less collistions.- if you go to wikipedia, you can read that
wis size of machine word. Here we do not really matter, what is this size, we can choose anyw > m. I chosem = 20.
So, everything is ready for function eval_hash(key): ((key*1031237) & (1<<20) - 1)>>5. Here I also used trick for fast bit operation modulo 2^t: for any s: s % (2^t) = s & (1<<t) - 1.
How our HashSet will look and work like:
- We create list of empty lists
self.arr = [[] for _ in range(1<<15)]. - If we want to
add(key), then we evaluate hash of this key and then add thiskeyto the placeself.arr[t]. However first we need to check if this element not it the list. Ideally, if we do not have collisions, length of allself.arr[i]will be1. - If we want to
remove(key)element, we first evaluate it hash, check corresponding list, and if we found element in this list, we remove it from this list. - Similar with
contains(key), just check if it is in list.
Complexity: easy question is about space complexity: it is O(2^15), because this is the size of our list. We have a lot of empty places in this list, but we still need memory to allocate this list of lists. Time complexity is a bit tricky. If we assume, that probability of collision is small, than it will be in average O(1). However it really depends on the size of our self.arr. If it is very big, probability is very small. If it is quite tight, it will increase. For example if we choose size 1000000, there will be no collisions at all, but you need a lot of memory. So, there will always be trade-off between memory and time complexity.
class MyHashSet:
def eval_hash(self, key):
return ((key*1031237) & (1<<20) - 1)>>5
def __init__(self):
self.arr = [[] for _ in range(1<<15)]
def add(self, key: int) -> None:
t = self.eval_hash(key)
if key not in self.arr[t]:
self.arr[t].append(key)
def remove(self, key: int) -> None:
t = self.eval_hash(key)
if key in self.arr[t]:
self.arr[t].remove(key)
def contains(self, key: int) -> bool:
t = self.eval_hash(key)
return key in self.arr[t]
If you like the solution, you can upvote it on leetcode discussion section: Problem 0705