https://leetcode.com/problems/find-the-duplicate-number

For me the main difficulty was that given tests are not clear at all: both of them have only one duplicate, however there can be examples like 2,2,2,2,3. Why there always will be duplicate? Because of Pigeonhole principle! Actually, it can be proven very easily: let us assume that it not correct: it means, that each number between 1 and n can have frequency only 0 of 1. It means, that there will be <= n numbers, but we need to have n+1. Contradiction: so, our assumption is correct: there will be at least one duplicate number.

One way to handle this problem is to sort data with O(n log n) time and O(n) memory or use hash table. Howerer it violates the conditions of problem: we can not use extra memory. There is smarter way and we need to use the fact that each integer is between 1 and n, which we did not use in sort.

Let us deal our list as linked list, where i is connected with nums[i]. Consider example 6, 2, 4, 1, 3, 2, 5, 2. Then we have the following singly-linked list: 0 -> 6 -> 5 -> 2 -> 4 -> 3 -> 1 -> 2 -> ... We start with index 0, look what is inside? it is number 6, so we look at index number 6, what is inside? Number 5 and so on. Look at the image below for better understanding. So the goal is to find loop in this linkes list. Why there will be always loop? Because nums[1] = nums[5] in our case, and similarly there will be always duplicate, and it is given that it is only one.

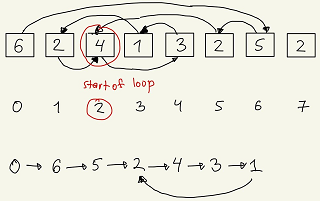
image

So now, the problem is to find the starting point of loop in singly-linked list (problem 142), which has a classical solution with two pointers: slow which moves one step at a time and fast, which moves two times at a time. To find this place we need to do it in two iterations: first we wait until fast pointer gains slow pointer and then we move slow pointer to the start and run them with the same speed and wait until they concide.

Complexity: Time complexity is O(n), because we potentially can traverse all list. Space complexity is O(1), because we actually do not use any extra space: our linked list is virtual.

class Solution:
    def findDuplicate(self, nums):
        slow, fast = nums[0], nums[0]
        while True:
            slow, fast = nums[slow], nums[nums[fast]]
            if slow == fast: break
           
        slow = nums[0];
        while slow != fast:
            slow, fast = nums[slow], nums[fast]
        return slow

Binary search solution

There is Binary Search solution with time complexity O(n log n) and space complexity O(1). We have numbers from 1 to n. Let us choose middle element m = n//2 and count number of elements in list, which are less or equal than m. If we have m+1 of them it means we need to search for duplicate in [1,m] range, else in [m+1,n] range. Each time we reduce searching range twice, but each time we go over all data. So overall complexity is O(n log n).

class Solution(object):
    def findDuplicate(self, nums):
        beg, end = 1, len(nums)-1
        
        while beg + 1 <= end:
            mid, count = (beg + end)//2, 0
            for num in nums:
                if num <= mid: count += 1        
            if count <= mid:
                beg = mid + 1
            else:
                end = mid
        return end

If you like the solution, you can upvote it on leetcode discussion section: Problem 0287